�@�P�j�@�N���u�̊������[�����g�l��
�@�@�X�C���O���̃N���u�̏d���l���͊ȗ��I�ɂ͎����ŕ\����A���̒l���傫���N���u�ق�
�@�@�U�蔲�����d���i���ׂ��傫���j�Ȃ�܂��B
�@�@�@�@�l�����v�E�i�`�|�Q�O�j�Q�^10000�@�i���E�u�j
�@�@�@�l���G�N���u�̊������[�����g�i���E�u�j
�@�@�@�@�v�@�G�N���u���ʁi���j
�@�@�@�@�`�@�G�o�����X�A�[���i�����j�o�d�S�_����O���b�v�G���h�܂ł̒����p
�@�@�@���G�㎮���e�Q�O�f�͗���̈��蕔���̒����̒萔�i�����j
�@�`�̓N���u�̃O���b�v�G���h����N���u�̏d�S�܂ł̒����ł���A�X�C���O��������
�@�N���u�̊������[�����g�l���̓N���u�̎����v�Ƃق��`�̓���ɔ�Ⴕ�Ă��܂��B
�@�d���N���u�̓o�����X�A�[���`�����������Ȃ�����l���̒l���傫���Ȃ��ĐU��Ȃ�
�@�Ȃ�܂��B
�@�l���̓X�C���O���̃N���u�̏d���ł����A�X�C���O���ɂ��v���N���u�̏d�S�ɏW�����A
�@�V���t�g�����Ȃ点��̂ł��B���̎��d�S�̈ʒu���������i�`���傫���قǁj�V���t�g��
�@���Ȃ�Ղ��Ȃ��A�V���t�g�̂��Ȃ�𗘗p�����X�C���O�ł͂`��傫�������N���u������
�@�L���ɂȂ�̂ł��B
�@�������A�`��傫��������l�����傫���Ȃ��X�C���O���̃N���u���d���Ȃ�̂��v���ӂł��B
�@�X�C���O���ɐg�̂�������N���u�̏d���i���ׁj�̊��o�́A�l���ł͂Ȃ��A
�@�l���^�i�`�|�Q�O�j�\��������ƍl���ėǂ��悤�ł��B�ܘ_�l���ɒ��������l�ł��B
�@�����l���^�i�`�|�Q�O�j�̒l�������N���u�͓����d�����o�ŃX�C���O���ł������Ƃ�
�@�����Ă���A�����l���X�C���O���o���o�l�@���@�ƌĂԂ��Ƃɂ��܂��B
�@
�p�^�[�������A�Z�b�g�̃N���u�ł͋@�\�I�E���o�I�Ɍ݂��ɗׂ荇���Ԏ肪�A���I��
�֘A��������̂��]�܂����̂͌����܂ł�����܂���B
�@���̗l�q�́A�X�C���O���ɃN���u�̒�����������o�����X�A�[���`����i�����j��
�@�X�C���O�����l�����y���N���u�̎����v�̒l���c���i�`�|�l���}�C�`�|�v�}�j�Ƃ���
�@�\���܂��B
�@�����̒l���݂��Ɋ֘A���Ă���̂ŁA�v�X���O���t�͓����l�q�̋Ȑ��ŕ`����܂��B
�@
�@���Ƃ��āA�ȉ����`�|�l���}�C�`�|�v�}�������܂��B�O���t�͈ȍ~�S�ĂT�����ł��B
�@�@�@�@�@
�@����͎��̃N���u�Z�b�g�̌���(�Q�O�P�R.�P�Q.�P�T)�̃f�[�^�Ɉ���O���t�ł��B
�@�E���珇�ɁA�P�v,�R�v,�T�v,�t�S�C�T�`�o���C�`��,�r��,�k��,�o���ł����A�E�b�h�ނ�
�@�V���t�g�̂��Ȃ����葽�����p���������߂ɂ`���A�܂��A�E�G�b�W�͐U�蔲�����y��
�@���邽�߂ɃV���t�g��Z��������ŁA�S�ẴN���u�̃O���b�v�̎��ʒ����ƁA������
�@��̃w�b�h�̎��ʒ����������������̂ł��B
�@�V���t�g�͑S�ăJ�[�{���V���t�g�̃t���b�N�X�͂q�ł����A�g���N�̓N���u�����k�ɔ����
�@���āA�����N���u�قǑ傫���i���Ȃ�₷���j�Z���N���u�قǏ������i���Ȃ��j
�@�Ȃ��Ă��܂��B
�@�����v���b�g�f�[�^�͒����O�̃I���W�i���̂��̂ł��B
�@�p�^�[�́A�U��N���u�ł͂Ȃ��̂ł����A�N���u�S�̂Ƃ̊֘A�͖����ł��܂���B
�@�O���t�͑S�ĂT�����Ȑ��ł��B�@
�`�|�l���}
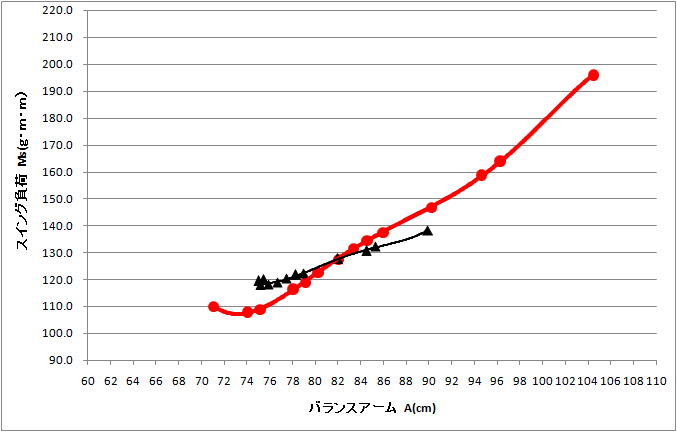
�@�S�̓I�ɃI���W�i���i���F�j�ɔ�ׂăo�����X�A�[���`���啝�Ɂi�E�Ɂj�L�сA�E�b�h�ł�
�@�������[�����g�l�����傫��(��Ɂj�Ȃ��Ă��āA�S�̓I�ɃN���u�Ԃ̃o�����X��������
�@���܂��B
�@�A�C�A���͈̔͂̒����ł́A�����̃o�����X�A�[���`���Ԋu���قڈ��ɂȂ��Ă��܂��B
�@�E�G�b�W�ނ͍D�݂ɂ���Ċ��o�I�ɔ����ɍ��ق�����A�X�C���O���̎�̊��o���d������
�@�g�̂ւ̕��ׂ�}���āi�l�����������j���܂����A�N���u�S�̂Ƃ̃f�[�^�̃o�����X��
�@��ł��B
�@���Ƀe�B�[�A�b�v���Ďg�p����P�v�́A�ő���̔������҂��ăV���t�g�̂��Ȃ��
�@�ő�����������ė��p���邽�߂��`��傫���A��������������l����傫�����Ă��܂��B
�@�����͔�͂ȂV�T�̎��Ȃ�ł͂̂��̂ŁA�̋�A�Z�́A�X�C���O�p�^�[�����ɂ���
�@�V���t�g�̍d�x�i�˂���g���N�j�A���ʁA�N���u�������ɂ��قȂ��Ă���͓̂��R�ł��B
�`�|�v�}
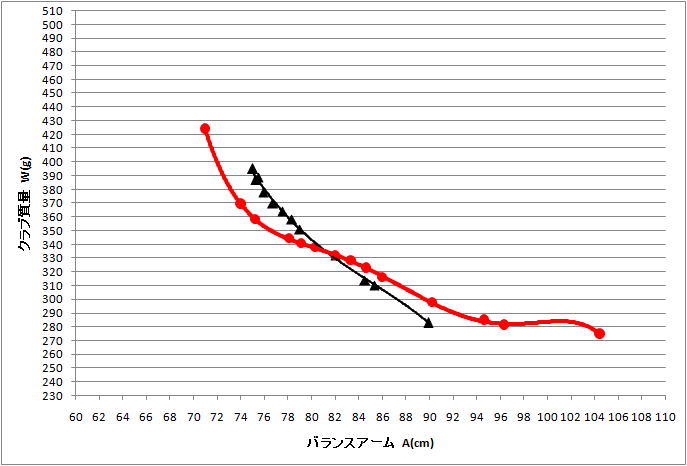
�@�@���̃I���W�i���ɔ�ׂđS�̓I�ɍ��E�ɐL�тĂ��āA�S�ẴN���u���y�ʂɂȂ��Ă���
�@�@�̂�������܂��B
�@�`�|�l���}�Ɠ��l�ɐ��R�ƃv���b�g������ł���̂����Ď��܂��B
�@
�@���Ȃ��̃N���u���`�C�l���C�v�̃f�[�^���O���t�ɕ`���Ă݂�ƁA���G�̗ǂ��N���u�Ԏ�
�@����ɂ��Č���ƁA�Ȑ�����O��Ă���Ԏ�̃N���u���������܂��B
�@�����Ȑ�����O��Ă���N���u��������̃N���u�̃X�C���O���o�͑��̃N���u�Ƃ͈قȂ���
�@����͂��ł��B���̌����́A�V���t�g�̎d�l�i�d����g���N�j���قȂ邩�A�o�����X�A�[���`
�@�Ԏ菇�ɂȂ��Ă��Ȃ��i�g���C�f���A�r���̑g�ݍ��킹���s�K���j���A�ł��B
�@�ܘ_����ł��V���b�g�̌��ʂ��ǂ���\��Ȃ��̂ł����A���ׂ̈�A�̃N���u�Ƃ��Ă�
�@�X�C���O���o�͈قȂ��Ă��܂�����A�ǂ����Ă��N���u�̘A�����ɂ����Ĉ�a�����c��܂��B
�@
�@���z�I�ɂ͂ǂ̃N���u�������悤�ȃX�C���O���o�ŃX�C���O�ł���A����ɉz�������Ƃ�
�@�Ȃ��̂ł�����A����Ƃ��f�[�^���O���t�����Ċm�F����邱�Ƃ������߂��܂��B
�Q�j�@�N���u�̃o�����X�A�[���`
�@�@�@�o�����X�A�[���`�́A�O���b�v�G���h����N���u�̏d�S�ʒu�܂ł̒����ł���A�N���u
�@�@�S�̂Ƃ��Ă͂��̏d�S�_�ɃN���u�̑S�d�ʂ��W�����Ă���ƍl���Ă悢�̂ŁA�X�C���O
�@�@���������������`�̒����̃N���u��U���Ă���悤�Ɋ�����̂ł��B
�@�@�܂��A�d�S�_�ɂ͓��R�N���u�̑S�d�ʂ��|����܂�����V���t�g�����Ȃ点��͓_�Ƃ�
�@�@�l�����܂��B
�@�@���̂悤�ɏd�S�_�̈ʒu�A����������o�����X�A�[���`�̒l���X�C���O���o�Ɠ�����
�@�@�V���t�g�̂��Ȃ�ɏd�v�ȗv���ƂȂ��Ă���̂ł��B
�@�@�����ŁA�o�����X�A�[���`��ω�������v�����l���Ă݂܂��傤�B
�@�@��̎��@�@�`���i�g���E�k�^�v�j�{�i�r���E�k�^�Q�v�j�{�i�f���E�f���^�Q�v�j
�@�@����N���u�����k���Œ肷��ƃw�b�h�̎��ʂg���Ńo�����X�A�[���`�̑傫���̍�����
�@�@���܂邱�Ƃ�������܂��B
�@�@�������A�g���C�r���C�f���̑����ω��ɂ��Ă͂ǂ��ł��傤���H
�@�@�����A�w�b�h���d������ꍇ�A�V���t�g���y������ꍇ�A�O���b�v���y������ꍇ�ł��B
�@�@��������`��傫������̂ł����A��ԑ傫������̂̓O���b�v���y������ꍇ�ŁA
�@�@���Ƀw�b�h���d������ꍇ�A�����ŃV���t�g���y������ꍇ�ƂȂ�܂��B
�@�@�����Œ��ڂ��ׂ����Ƃ́A�w�b�h�̏ꍇ�ɂ̓N���u���d�ʂ̑������O���b�v��V���t�g��
�@�@�ꍇ�Ƃ͔��ɂȂ����Ƃł��B
�@�@�����A���ɂf���̑������`�̑傫���̑����ɑ傫���֗^���Ă���A�N���u���d������
�@�@�`�����������A�N���u���y�������`��傫������̂ł��B
�@�@�g���̑������`�̑����Ɋ֗^���܂����A���̉e���͂f�������y���ɏ��Ȃ��A������
�@�@�N���u�̑��d�ʂ̕ω����t�ɂȂ�A�N���u���d�������`��傫�����A�N���u���y������
�@�@�`������������̂ł��B
�@�@���̌��ۂ̓N���u�̒����ɂ͔��ɏd�v�Ȃ��ƂŁA�O���b�v�ƃw�b�h�̎��ʒ�����
�@�@�N���u�̃X�C���O���o�ɔ��ɏd�v�ȃo�����X�A�[���`�����ʓI�ɒ������邱�Ƃ�
�@�@�ł���̂ł��B
�R�j�@�V���t�g�̂��Ȃ�
�@�@�{�[���������֔����̏����́A�{�[���q�b�g���̃w�b�h�X�s�[�h��傫������
�@�@���Ƃł����A����ɂ̓X�C���O�X�s�[�h��傫�����邱�Ƃ̑��ɁA�V���t�g�̂��Ȃ��
�@�@���p���ă{�[���q�b�g�̏u�ԂɃw�b�h�X�s�[�h�����������邱�Ƃł��B
�@�@���Ɉ�ʃA�}�`���A�����͂ȃV�j�A�⏗���ɂ͂��̃V���t�g�̂��Ȃ�𗘗p���邱�Ƃ�
�@�@���ɗL���ȗv���ƂȂ�܂��B
�@�@�{�[���̔��ƕ������ɑ傫���W����V���t�g�̂��Ȃ�Ɲ�����́A���ɂ��Ȃ��
�@�@���x�ɂ��Ă͎��̎O�̗v���ɂ��܂��B
�@�@�@�@�V���t�g�̍ގ��ɂ�邵�Ȃ�
�@�@�@�@�ގ��̕����l�ɂ���炩�����́i���Ȃ�Ղ��j����d�����́i���Ȃ��j�܂�
�@�@�@�@����܂��B�ގ��̓J�[�{������X�e�B�[���܂ł���A�v�X�ɍd�x�̒��x���\�������
�@�@�@�@���܂��B
�@�@�A�@�V���t�g�̍\���ɂ�邵�Ȃ�
�@�@�@�@�V���t�g���I�ɓ��ɂ��Ȃ�Ղ������\���̂��̂ŁA���̏ꏊ�ɂ���ʓI��
�@�@�@�@�撲�q�i�w�b�h�ɋ߂������j�A�����q�i�V���t�g���������j�A�茳���q�i�O���b�v
�@�@�@�@�ɋ߂������j�ƕ\������Ă��܂����A�ŋ߂͂��̗v�f�̌������i�݁A�X�ɂ��ߍׂ���
�@�@�@�@���Ȃ萫�\�̕��z���𖾂���Ă��Ă���A�V���t�g�I�тɔ��ɗL���ł��B
�@�@�B�@�N���u�̊����͂ɂ�邵�Ȃ�
�@�@�@�@�X�C���O�������̃N���u���̂̊����͂ɂ��V���t�g�����Ȃ錻�ۂł���A
�@�@�@�@�o�����X�A�[���i�`�j���傫���֗^���邵�Ȃ�ł��B
�@�@�ȏ�A�V���t�g�̂��Ȃ�̎O�̗v���ɂ͕v�X�ɓ���������A�@����{�Ƃ��āA
�@�@�A�ƇB�̑g�ݍ��킹��K�ɂ��邱�Ƃɂ��œK�ȃN���u�Ɏd�グ�邱�Ƃ��ł��܂��B
�@�@�����ŁA�o�����X�A�[���i�`�j�ƃN���u�S���i�k�j�̊W�ɂ��čl���Ă݂܂��傤�B
�@�@�X�C���O�������N���u�̑��d�ʂ��d�S�_�ɓ����V���t�g�����Ȃ点����ʂ�����̂ŁA
�@�@�傫���`�̃N���u�͂��ꂾ���傫���V���t�g�����Ȃ点�邱�Ƃ����҂ł��܂��B
�@
�@�@�N���u�̍\���v�f�ł���w�b�h�A�V���t�g�A�O���b�v�̍œK�g�ݍ��킹�ɂ����āA
�@�@�`�Ƃk�̊W���i�N�T�����ė��܂������A�قڎ��̂悤�ȊW�����邱�ɓ��B���܂����B
�@�@�@�@�@�i�`�|�U�O�j�^�i�k�|�V�O�j�̒l���傫���قǃV���t�g�����Ȃ点�Ղ�
�@�@���̒l���V���t�g�����Ȃ�W�����ƌĂԂ��Ƃɂ��܂��B
�@�@
�`�|�k�}
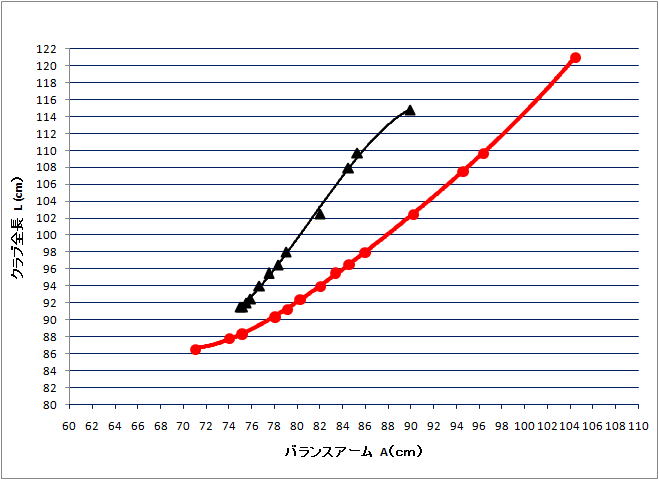
�@�I���W�i�������A�P�v�̓V���t�g�������Ă��܂��B�E�G�b�W�ވȉ��̓V���t�g��Z�߂�
�@���Ă��܂��B
�@���̃O���t�ł����R�ƃf�[�^���Ȑ���ɕ���ł���̂��悭������܂��B
�@
�@�@�ȏ�A�`���k�̊W�̓V���t�g�̂��Ȃ���������Ŕ��ɏd�v�ȗv�f�ł��B
�@�@�X�C���O�ŃV���t�g�̂��Ȃ���ő�����o���ăw�b�h�������N���u�̕��@�́A�N���u��
�@�@�S���k�ɑ��ăo�����X�A�[���`���ő���ɑ傫�����邱�Ƃł��B
�@�@�������A�`��傫������ƑO�q���l���̒l���傫���Ȃ��Ă��܂�����Ȃ�̗̑͂�
�@�@�Z�ʂ��K�v�ƂȂ�܂��̂ŁA�����̌��E�̂l���A�l���^�i�`�|�Q�O�j�̒l���m�F���Ă���
�@�@���̌��x���ł`�����߂��K�v������܂��B
|



![]()
